Thin walled Pressure vessel Concept

Thin walled Pressure vessel:-

What is pressure Vessel?

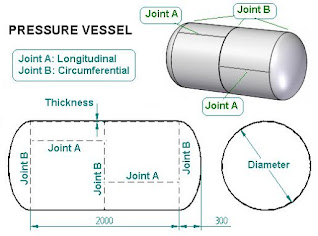
Pressure vessel is defined as closed cylindrical or spherical container which is designed to hold or to store fluids at pressure substantially different from ambient pressure.

Classification of Pressure Vessel.

1.based on d/t ratio:-

1.Pressure vessel whose d/t ratio is greater than 20 units, such type of vessel is categorized to Thin walled pressure vessel (d/t ≥ 20).

Ex. Boiler shell, LPG cylinder pressure cooker, storage tank 

2.  Pressure vessel whose d/t ratio is less than 20 units, such type is called as Thick walled pressure vessel (d/t≤ 20).

Ex. Hydraulic cylinder, gun Barrel, Storage tank under high pressure

2. Based on Shape of shell

1.   Cylindrical pressure vessel

2.   Spherical pressure vessel

DO comment !!!!!!

1.Why Spherical vessel better then cylindrical pressure vessel?
2.Which vessel we should used for safety purpose?
3.Which vessel we should used, keeping manufacturing cost in  mind?

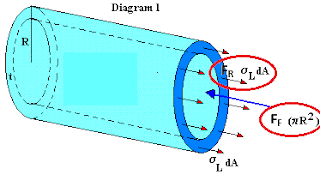
Bursting of  pressure vessel occurs circumferential. 

Condition-1

At particular pressure, when longitudinal stress in thin walled pressure vessel is greater than ultimate strength, circumferential bursting occurs in pressure vessel.

σL> sut

FF = FR

  

FF= (π D2 P)/4-------------------------------i

FR= σLxπ𝐷x𝑡--------------------------ii

(π D2 P)/4 = σLxπ𝐷x𝑡

σL= σ2= σlongitudinal = pd/4t = σ1/2

Bursting of  pressure vessel occurs longitudinally.

 

Condition-2

At particular pressure, when Hoops stress in thin walled pressure vessel is greater than ultimate strength, bursting occurs longitudinally in pressure vessel.

σh> sut

FF = 2xFR 

FF= PxLxD-------------------------------i

FR= 2xσhxLxt--------------------------ii

PxLxD= 2xσhxLxt 

σh = σ1 = σhoop = pd/2t

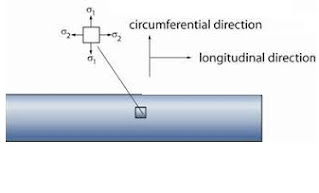
Thin pressure vessel can be considered bi axial state of stress (due to longitudinal stress).

σ1 = σhoop = pd/2t

σ2 = σlongitudinal = pd/4t = σ1/2

In plane τmax

=(σ1-σ2)/2 = pd/8t

Absolute τmax

=σ1/2 = pd/4t

Strain stress

Major principal strain 

ε1=εhoop= δD/D----------i

ε1= 1/E [σ1-μσ2]-----ii

σ2 = pd/4t = σ1/2

Equating i & ii

εh=δD/D=σ1/2E x[2-μ]

εh =pd/4tEx[2-μ]

 

Minor principal strain

  ε2=ε longitudinal= δL/L----------i

ε2= 1/E [σ2-μσ1]-------------ii

σ2 = pd/4t = σ1/2

Equating i & ii

 εL=δL/L=σ1/2E x[1-2μ]

εL = pd/4tEx[1-2μ]

Volumetric strain

δV/V=pd/4tEx[5-4μ]

Thickness of the shell

Safe condition of design (σ max⁡)ind ≤(σt )per

σ hoop⁡ ≤(σt )per 

σ hoop⁡ cylindrical=pd/2t  ≤ (σt )per

σ hoop⁡ spherical=pd/4t  ≤ (σt )per 

Thin C.P.V

According to failure theory (MPST,MSST)

PD/2t= ≤(σt )per

t ≥PD/2(σt)per+corrosion Added

Thin S.P.V

According to failure theory (MPST,MSST,MDET)

PD/4t= ≤(σt )per

t ≥PD/4(σt)per+corrosion Added

Refer Static Structure Analysis for thin Pressure Vessel in Ansys for better understanding .

Static Structure analysis of Pressure vessel in Ansys 

AISC's Structural Steel Shapes

Structural steel design  is an area of knowledge of structural engineering where we used to design steel structures. The structures can range from schools to homes to bridges. Structures such as buildings, bridges, aircraft and ships are all examples which comes under steel structure. 

The effects  cause on structure due to application of load is determine through structural analysis Strength of materials is the branch of engineering which deals with the study of structural design. Engineering software such as STADD Pro, TEKLA , SACS, ANSYS  etc.  are used to analyze their strength. 

Basically  Steel structure is steel construction material with a unique  profile and  a specific shape or cross section with certain standards of chemical composition and mechanical properties.

The American Institute of Steel Construction (AI SC), Inc. publishes the Steel Construction Manual (Steel construction manual, or SCM), which is currently in its 14th edition. Structural engineers use this manual in analyzing, and designing various steel structures.

The mentioned link will give you the complete description of AISC 's structural steel shapes in the US  and will provide you the reference to determine the availability and engineering design data of specific structural steel shapes.

(Click Here) Link:- AISC Structural Shapes

Click above link to find ASIC Structural Shape Properties 

Source:-

https://en.wikipedia.org/wiki
http://www.engineersedge.com

Shear and Bending Moment diagrams

Shear and Bending Moment diagrams

Bending Moment -

It is reaction produce in a element when an external force or moment is applied to the element which causes elements to bends.

Shear Force - 

force acting parallel to the cross section of elements or acting along the plane is      called a shear force or shearing force.

Below is the Link provided for Shear Force and Bending Moment Diagram Calculation of a Beam:-

Below I am showing how to calculate shear force and bending moment diagram. you can find many link for calculating bending moment diagram for different loading and support. example i          have show  below for one condition.

Be care full about units of input data to get the correct result.

Finite Element Analysis of Composite Sandwich Panel Under Static Load condition

Definition of composite material terminology:-

composite materials:- 

A Composite material is a material made from two or more constituent materials with different physical or chemical properties .when it is combined it produces a material with characteristics different from the individual components.

Orthotropic martial:-

Orthotropic materials have material properties that differ along three mutually-orthogonal twofold axes of rotational symmetry and their properties change when measured from different directions.

Anisotropy:-

 is the property of material which depends on direction, which implies different properties in different directions, opposite to that of  isotropy. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties.

Catia V5 Introduction

Catia V5 Introduction